NSFD
- nbairagi
- Sep 7, 2020
- 2 min read
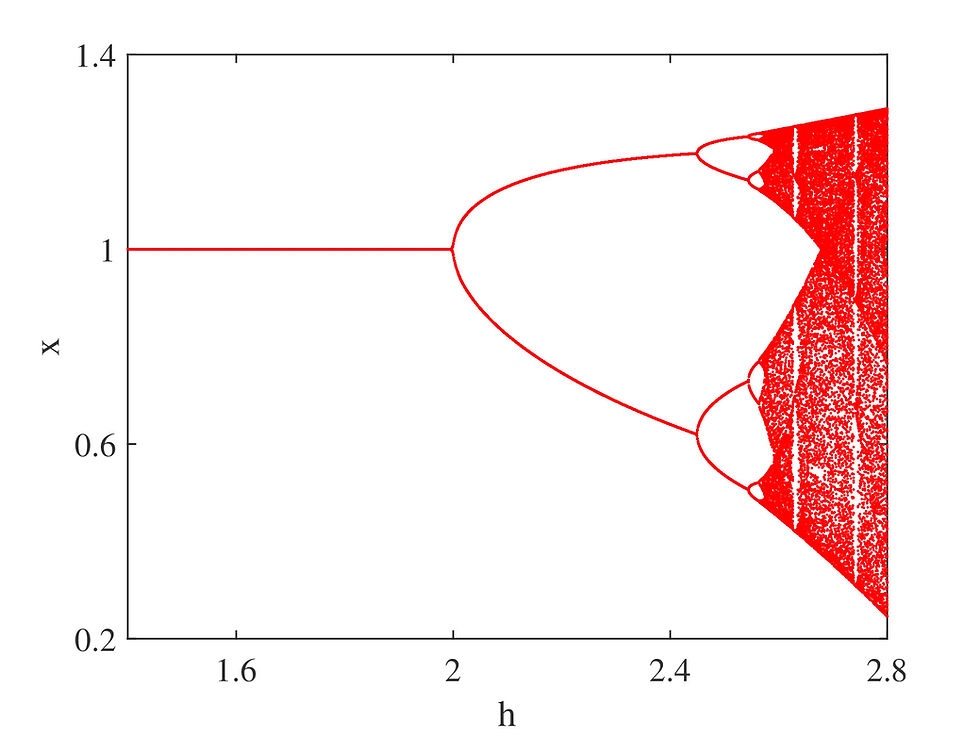
Discretization of nonlinear ordinary differential equations is important because it, in general, cannot be solved and therefore discretization is inevitable for good approximation of the solutions, and secondly discrete models permits arbitrary time-step units. However, conventional discretization schemes, such as Euler method, Runge-Kutta method, produces spurious solutions which are not observed in its parent model and its dynamics depend on the step-size. For example, the dynamics of logistic differential equation in continuous system is very simple: any solution starting with positive initial value reaches to nontrivial equilibrium point, implying that the nontrivial equilibrium point is stable. Dynamics of the corresponding discrete logistic model formulated by Euler forward method is, however, very complex. The nontrivial equilibrium point is stable if the step-size is relatively small. The system shows very complicated period doubling bifurcation to chaos as the step-size is gradually increased. Thus the dynamics of the discrete model depends on the step-size. Another important drawback of the conventional discrete model is that the positivity of its solutions does not hold for all positive initial values. Any finite-difference scheme that allows negative solutions will have numerical instabilities. So the following questions arise: (i) Can you construct a discrete system which will show the exact behavior of the corresponding continuous system? (ii) Are the solutions of the proposed discrete model remain positive for all positive initial conditions? (ii) Are the dynamics of the system independent of the step-size?
For such dynamic preserving discretization of the continuous-time system, one can go for non-standard finite difference (NSFD) scheme introduced by Mickens in 1989. A finite difference scheme is called non-standard finite difference (NSFD) method if at least one of the following conditions is met: (1) denominator functions for the discrete derivatives must, in general, be expressed in terms of more complicated functions of the step-sizes than those conventionally used, (2) nonlinear terms should, in general, be replaced by non-local discrete representation, i.e. by a suitable function of several points of mesh.
In this project, I would like to propose some dynamics preserving NSFD models (dimension) of nonlinear biological phenomena. It will be shown that all the dynamic properties of NSFD models are identical with the corresponding continuous models. It will also be shown that the proposed discrete models are robust even when the discretization time-step is large.





Comments